用鼠標和貝塞爾曲線交互

貝塞爾曲線（The Bézier Curves），是一種在計算機圖形學中相當重要的參數曲線（2D，3D的稱為曲面）。貝塞爾曲線于1962年，由法國工程師皮埃爾·貝塞爾（Pierre Bézier）所發表，他運用貝塞爾曲線來為汽車的主體進行設計。

線性曲線
給定點P0、P1，線性貝塞爾曲線只是一條兩點之間的直線。這條線由下式給出：

當參數t變化時，其過程如下：

線性貝塞爾曲線函數中的t會經過由P0至P1的B（t）所描述的曲線。例如當t=0.25時，B（t）即一條由點P0至P1路徑的四分之一處。就像由0至1的連續t，B（t）描述一條由P0至P1的直線。
二次曲線
二次方貝塞爾曲線的路徑由給定點P0、P1、P2的函數B（t）追蹤：

為建構二次貝塞爾曲線，可以中介點Q0和Q1作為由0至1的t：
* 由P0至P1的連續點Q0，描述一條線性貝塞爾曲線。
* 由P1至P2的連續點Q1，描述一條線性貝塞爾曲線。
* 由Q0至Q1的連續點B（t），描述一條二次貝塞爾曲線。
二次曲線看起來就是這樣的：

三次曲線
為建構高階曲線，便需要相應更多的中介點。對于三次曲線，可由線性貝塞爾曲線描述的中介點Q0、Q1、Q2，和由二次曲線描述的點R0、R1所建構。
P0、P1、P2、P3四個點在平面或在三維空間中定義了三次方貝塞爾曲線。曲線起始于P0走向P1，并從P2的方向來到P3。一般不會經過P1或P2；這兩個點只是在那里提供方向資訊。P0和P1之間的間距，決定了曲線在轉而趨進P3之前，走向P2方向的“長度有多長”。
曲線的參數形式為：

看起來就是這樣的：

高階曲線
更高階的貝塞爾曲線，可以用以下公式表示：
用表示由點P0、P1、…、Pn所決定的貝塞爾曲線。則有：

更多的關于貝塞爾曲線的內容，你可以去查閱各種數學書。加油，求知的騷年。
應用
在幾乎所有的高級圖像軟件中，均使用到了三次貝塞爾曲線來實現“平滑曲線”繪制功能。例如photoshop中的“鋼筆”，CoralDraw中的“貝塞爾工具”，Fireworks中的“畫筆”。

在編程中實現
計算機繪圖
要“畫”出貝塞爾曲線，一般需要進行較多的計算，然后繪制出來，類似這樣：

繪制的代碼可以在各類計算機圖形學書籍中找到。
GDI+
幸運的是，GDI+已經封裝好了貝塞爾曲線的繪制代碼，如果你想畫出貝塞爾曲線，只用調用Graphics.DrawBezier方法：

這是一個三次貝塞爾曲線，其中4個點分別為：起點，起點控制點，終點，終點控制點。繪制出來的效果如下：

與鼠標的交互
怎么實現Photoshop里那樣可以調整的貝塞爾曲線呢？兩種方法：
* 輸入新參數生成曲線
* 用鼠標交互調整曲線
很顯然第二種看起來會拉風很多，那么就來試試看。
你想要獲得是這樣的效果：

這是一條三次貝塞爾曲線，圖中應該這樣解讀：

所以需要幾個需要解決的：
* 表示貝塞爾曲線的錨點和控制點
* 繪制曲線和控制點/控制柄
* 鼠標交互
看起來不是很難的樣子，那么就來化整為零，各個擊破吧。
錨點
對于三次貝塞爾曲線而言，有兩個錨點：起始點和結束點。每個錨點有兩個坐標：本身坐標和控制點坐標。于是，可以用這樣的類來描述：

三次貝塞爾曲線
三次曲線前面已經說過原理了，那么它的結構應該就是這樣的：

畫出來
為了簡單，就用一個最基本的渲染器來畫，代碼如下：

畫出曲線和控制點及其手柄：


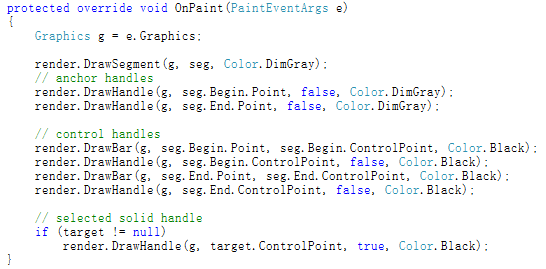
畫出來的效果就是這樣的：

鼠標交互
和鼠標實際上是這樣交互的：
* 按下鼠標，如果落點在某個控制點上，就表示選中了該點，否則落空
* 移動鼠標，如果選中了某個控制點，則調整控制點坐標至新坐標，否則忽略
* 放開鼠標，取消任何選擇
看起來只需要處理MouseDown，MouseMove和MouseUp這三個事件就夠了，很容易嘛。
先弄一個全局標記：

然后處理鼠標事件：
MouseDown：

MouseMove：

MouseUp：

為了簡單，刷新就這么弄了：

更高效的刷新應該只處理臟區。
效果
最后看起來就像這樣。

就這么簡單。

擴展和優化
要實現Photoshop那種曲線效果，需要多個錨點連接起來。上面的方法在效率上也還有可以提高的地方。